When given an equation of a function, there are a few simple domain rules that you must identify.
- The domain of any polynomial function is all real numbers.
- The denominator of a rational function cannot equal 0.
- Expressions inside of a radicand (√) cannot be negative.
Once you identify which rule applies to the given function, finding domain becomes very simple.
Domain of a Polynomial Function
As mentioned above, the domain of any polynomial is all real numbers. We can represent this in two different notations.
First is set notation. Here is an example of what set notation looks like:
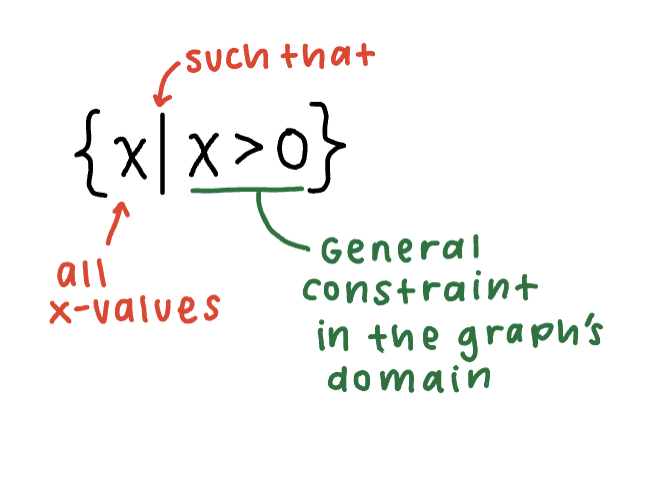
So, when representing the domain of all real numbers, set notation would look like:

The second way to represent domain is interval notation. Interval notation is based off of a number line and is a simple way to represent inequalities.
Write the beginning and ending numbers of the interval included in the domain, using a closed bracket if the endpoint is included or an open parentheses if it isn’t. To include multiple intervals in the domain, use the union symbol (U) in between.
Here is an example of what interval notation looks like:
So, when representing the domain of all real numbers, interval notation would look like:
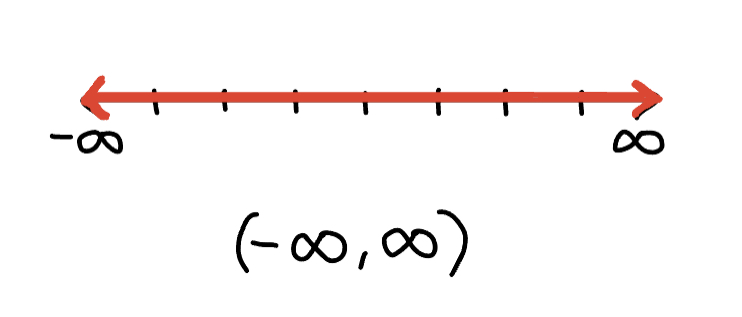
Domain of a Rational Function
Since you cannot divide any number by 0, the denominator of any function must not equal 0.
Therefore, your first step is to set the expression in the denominator equal to 0. In doing so, you are finding which numbers make the function undefined (and are NOT included in the domain).
Once you have set the denominator equal to 0, solve for x. In most cases, there will be multiple values of x that make the expression equal to 0. You can find all of these values by factoring and setting each factor equal to 0.
Now that you have determined all of the x-values that make the denominator equal to 0, you are done! Just write the domain using either set or interval notation, making sure to exclude these values.
Here is an example:

Domain of a Radical Function
Remember – expressions inside of a radicand (√) cannot be negative (but they can still be 0).
Therefore, your first step is to set the expression inside of the radicand greater than or equal to 0. In doing so, you are finding the x-values that make the expression positive, and excluding the values that make it negative from the domain.
Then, solve for x. When solving inequalities, treat the inequality symbol like an equal sign – however, DON’T forget to flip the inequality sign when dividing or multiplying both sides by a negative value.
Here is a simple example:

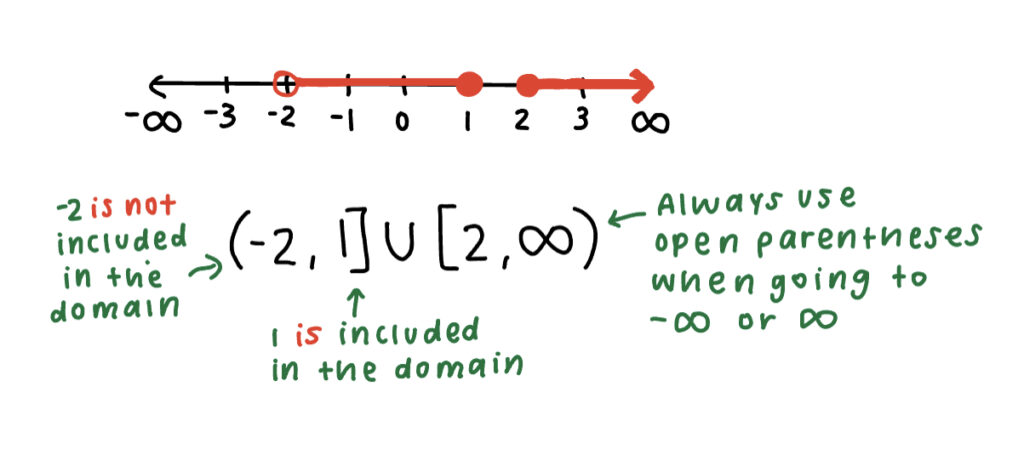
However, radical functions can get a lot more complicated. In situations where you end up with multiple x-values that equate the expression to 0, you will have to plot points on a number line. Then, you will have to test a number in between each interval to determine if the interval is positive or negative.
Positive intervals are included in the domain, while negative intervals are excluded.
Here is an example:

Domain of a Rational AND Radical Function
When you have a radical inside of a rational function, you will have to apply both rules and determine a domain that satisfies both conditions.
When faced with two domains with inequalities, simply choose the one that is more restrictive. If both domains can exist at the same time, combine them.
Here is an example:
